プログラミング初心者の子供に何を教えたらいいの？とお悩みの保護者のためのScratch（スクラッチ）の入門講座。Scratchで猫の動かし方はわかったけど・・・次にどんなことをしたらいいの？という疑問にお答えするシリーズです。
プログラミングがすごくできる方に「子供の時に、プログラミングで何してたんですか？」と聞いたことがあります。
その方曰く「虹色のう◯こを書いて遊んでいた」そうです・・・・・。
何か絵を描くというのはとても楽しいことですし、出来上がったときの達成感も得られそうです。
今回は幾何学模様の原点に立ち返って絵を描きながら数学のことも学んでしまいましょう！
以前、様々な幾何学模様を描いた記事を書いていますのでそちらも参考にしてみてください。
＜プログラミング初心者のためのScratch（スクラッチ）入門-ペン編（５）＞
＜プログラミング初心者のためのScratch（スクラッチ）入門-ペン編（６）＞
＜プログラミング初心者のためのScratch（スクラッチ）入門-ペン編（７）＞
1. サイクロイドを描こう
1-1. サイクロイドって何？
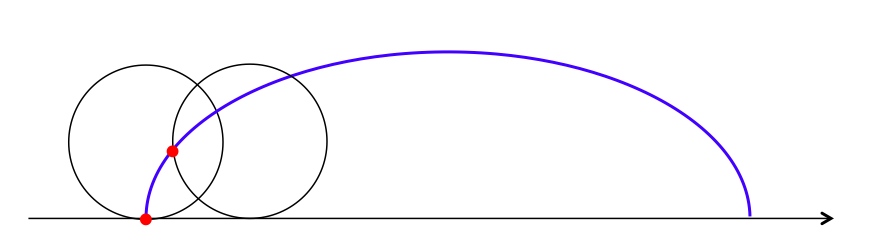
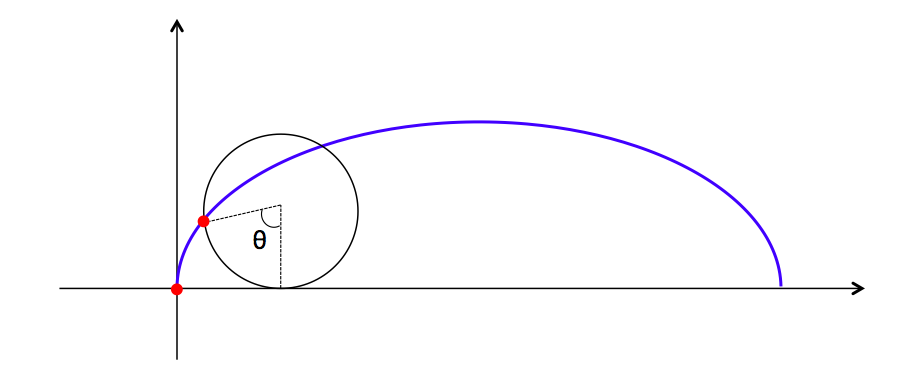
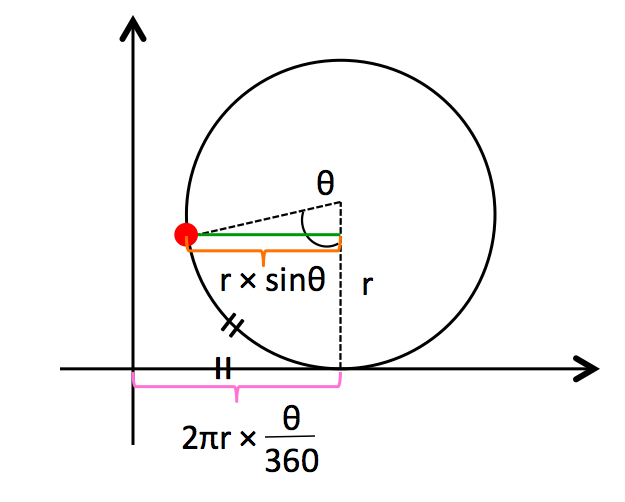
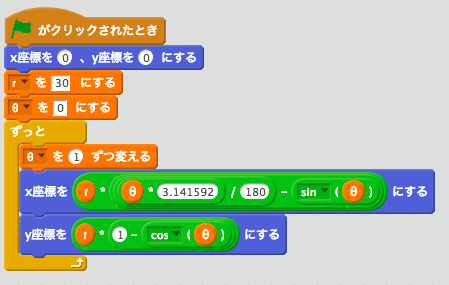
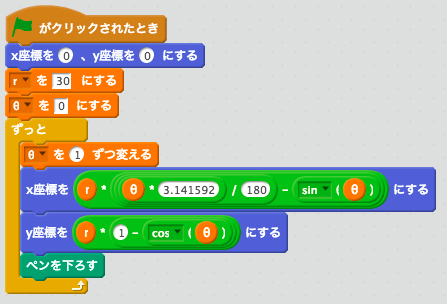
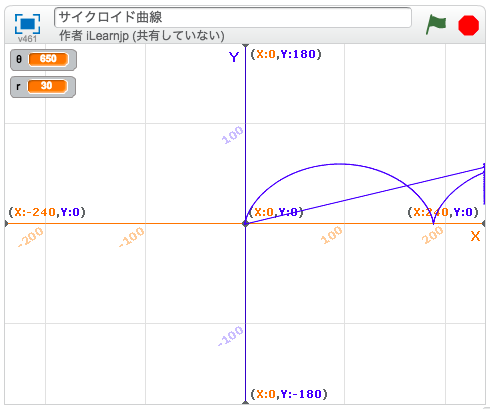
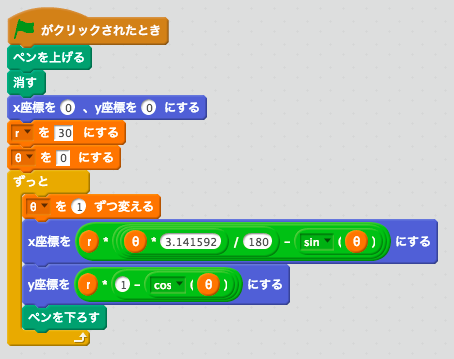
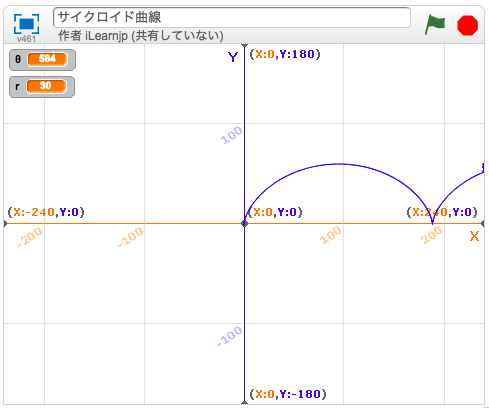
幾何学模様が作れる曲線について調べていると「サイクロイド」という言葉をよく目にします。では、サイクロイドとはいったいどんな曲線なのでしょうか？
たとえば、下の図のように円と直線があります。この円が、直線の上を滑らずに転がっていきます。
円が直線の上を転がる時、上の図の赤い点の動きがサイクロイド曲線になります。
▼サイクロイド曲線イメージ図
この円の半径がr、回転した角度θ（単位は度（※注））としたときのx座標とy座標を求めてみましょう。
まずはx座標から求めましょう。上の図の一部を拡大してみました。赤い点のx座標は、下の図の（ピンク色の部分）-（オレンジ色の部分）となります。
ピンク色の部分は、θ度の扇型の部分の長さと同じなので2πr×θ°/360° となります。
また、オレンジ色の部分は三角関数を使って計算できるので、r×sinθ°となります。
したがって、半径rの円がθ度転がったときのx座標の式は次のようになります。
※ただし、θの単位は度。
次にy座標の式を求めましょう。
赤い点のy座標は、下の図の（半径r）ー（オレンジ色の部分）となります。オレンジ色の部分は三角関数を使うとr
オレンジ色の部分は三角関数を使うとr×cosθ°となるので、y座標の式は次のようになります。
※ただし、θの単位は度。
1-2. Scratchでサイクロイドを描こう
サイクロイドについて、なんとなく理解できたところでScratchで数式を作ってみたいと思います。
新しくスクラッチのプロジェクトを作成する画面を立ち上げたら、ネコは削除しておきましょう。そして、背景をグラフ用紙にし、絵のないスプライトを準備します。
次に変数「r」と「θ」を作りましょう。そのあとにこの変数を使って、サイクロイドの式を作ります。上がxの式で下がyの式です。
この式で、rは円の半径なので変化しません。rには好きな数を入れられるようにプログラムを作ります。
そして、θは円が転がったときの角度なので、どんどん変わっていきます。最初が0でずっと変わり続けるようにするためにはつぎのようなプログラムにします。
ここに、x座標とy座標が、先ほど作った式の通りになるようにプログラムを追加します。
最後に、ペンで線を描く部分を足したらサイクロイドを描くプログラムの完成です。
このプログラムを実行すると・・・・あら、余計な線が入ってしまっています。
最初に余計な線を綺麗にしておく処理を追加しておきましょう。
これで余計な線が描かれることがなくなりました。
1-3. 大きさとスタート地点を変えて遊ぼう
せっかく作ったサイクロイド曲線ですが、大きさをもっと小さくして何回も曲線を描くようにしたいですね。
そこで大きさ＝円の半径とθの値をいろいろ変えてみたいと思います。
プログラムのここの数値を変えます。
半径r=10, θの最初の値=-1080にすると、小さいサイクロイドができました。
半径r=15, θの最初の値=-720にすると、先ほどより少し大きくなりました。
2. トコロイドを描こう
2-1. トコロイドって何？
トコロイドはサイクロイドの親戚です。先ほどのサイクロイドは円の上の点（図の赤い点）の軌跡でしたが、
トコロイドは円の外側の点（図の緑色の点）の軌跡を描いたものになります。
内側の円（実線の円）の半径をrm、外側の円（点線の円）の半径をrdとしたとき、この円がθ度転がったときの緑色の点のx座標とy座標の式は次のようになります。
2-2. Scratchでトコロイドを描こう
サイクロイドの時と同じように、変数rmとrd、そしてθを作り計算ブロックでトコロイドの式を作ります。
そして、これを先ほどのサイクロイドのプログラムと同じように作ればOK。今回は別の色でトコロイドを描きたかったので、ペンの色を変えるようにしました。
このプログラムを実行した結果がこちら。
サイクロイドに似ていますが、x軸のあたりでくるんと一回転しているところが違います。
2-3. 大きさとスタート地点を変えて遊ぼう
サイクロイドの時と同様に、トコロイド曲線の大きさなどを変えて遊んでみましょう。
rd=25、rm=15、θの最初の値=-720にすると小さなトコロイドが描けました。
いままで、rd>rmとなるように値を設定してきましたが、
rd < rmとしたらどうなるでしょうか？
rd=10、rm=20、θの最初の値=-720にしてみましょう。すると・・・x軸付近のくるくるがなくなり、波のような曲線を描くことができました。
サイクロイド曲線とトコロイド曲線を描くプログラムはこちらにありますので、いろいろ遊んでみてくださいね。
3. まとめ
今回は、幾何学模様の基本となりそうなサイクロイド曲線とトコロイド曲線をScratchで描いてみました。
式はちょっと難しいですが、どんな曲線かわかればそれで大丈夫ですよ。
・サイクロイドは、直線を転がる円の円周上の点
・トコロイドは、直線を転がる円の外（もしくは中）の点
が描く軌跡の曲線でした。
今回は「直線」の上を円が転がりましたが、転がる場所が円の外だったり中だったりすると、
また違った曲線が描けるのでまたの機会にそちらも解説してみたいと思います。
