プログラミング初心者の子供に何を教えたらいいの?とお悩みの保護者・先生のためのScratch(スクラッチ)の入門講座。Scratchで猫の動かし方はわかったけど・・・次にどんなことをしたらいいの?という疑問にお答えするシリーズです。
今回は「再帰」について考えてみたいと思います。再帰プログラムを使って、フラクタル図形の一つである「コッホ曲線」をScratchで描いてみます。
1. 再帰とフラクタル
再帰??フラクタル??聞いたことがある人もいるかもしれませんね。聞いたことがない人にはなんだか難しそうな言葉が出てきましたが、わかってもらえるよう頑張って解説してみたいと思います!
1-1. 再帰とは?
再帰(さいき)とは、何かについて記述するときにそのもの自身を呼び出すことです。例えば、「ナスはナス科の植物です」という説明をしているような感じでしょうか。
まだよくわからないと思うので、次のプログラムを見てください。
コッホ曲線という曲線を描くための「定義」ブロックです。定義の中に、自分自身(赤枠の部分)が入っているのがわかるでしょうか。このように、自分の定義に自分が含まれているプログラムを再帰プログラムと言います。
▼コッホ曲線の定義の一例

1-2. フラクタルとは?
フラクタルとは、あるもの一部分が、そのもの全体と似ているような図形のことを言います。別の言い方をすれば、あるフラクタル図形の一部分を拡大していくと全体と同じ形が現れる、ということです。フラクタルの図形として有名なものには以下のようなものがあります。
・コッホ曲線
・シェルピンスキーのギャスケット
など
また、自然界においてもフラクタルのような性質を持つものがたくさん発見されています。
・ロマネスコというブロッコリーの一種
・血管の分岐構造
・海岸線
・雲の形
これらも「フラクタル」だそうです。
このフラクタルは、再帰プログラムで描くことができます。そのため、再帰プログラムの理解のためにフラクタル図形を描くことはとても多いのです。
1-3. コッホ曲線とは?
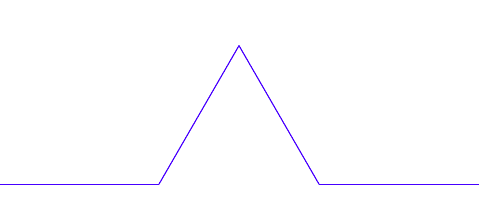
コッホ曲線とはこういう曲線です。

この曲線の描き方を順を追って解説します。最初に直線があります。

この直線を3等分します。

この3等分したところの真ん中の部分に正三角形を描いて、下の線を消します。そうすると、4つの直線ができますね。
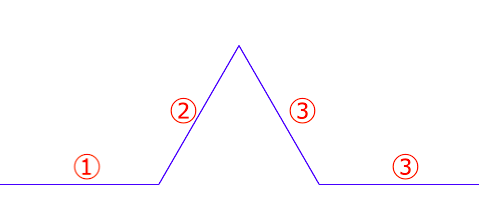
この直線にそれぞれに対して、同じ操作を繰り返します。するとこのような図形になり、また直線が増えました。直線の数は全部で16本です。

さらにこの16本の直線に対して同じ操作を繰り返すとこのようになります。
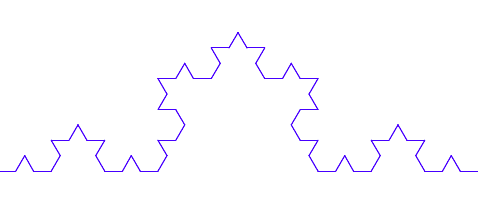
これを繰り返していくことで得られる曲線がこちらです。

2. コッホ曲線をScratchで描こう
言葉の定義がわかったところで、いよいよ実践です。
2-1. 再帰を使わないプログラムを作ってみる
再帰プログラムを考える前に、ペンを使ってコッホ曲線最初の図形を無理やり描いてみましょう。
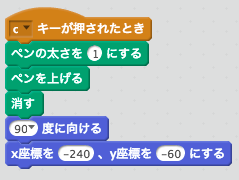
最初に、絵のないスプライトを準備します。そして、画面をリセットするプログラムを作っておきます。
このプログラムは、cキーを押して実行します。ペンで描いた線を消し、スプライトの位置を元の場所に戻してくれます。
次に、再帰回数が0回の線を描きます。コッホ曲線の全体の長さを変数「長さ」で表しています。
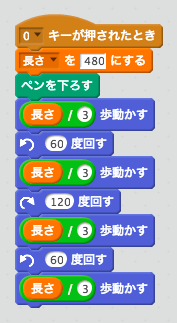
0キーを押してこのプログラムを実行すると、再帰回数0回の線が描かれます。
次に、再帰回数1回の曲線を描くプログラムを作ってみたいと思います。
考え方はこうです。先ほどの再帰回数0回のプログラムの「●歩動かす」の部分に長さを3分の1した同じプログラムを入れていきます。
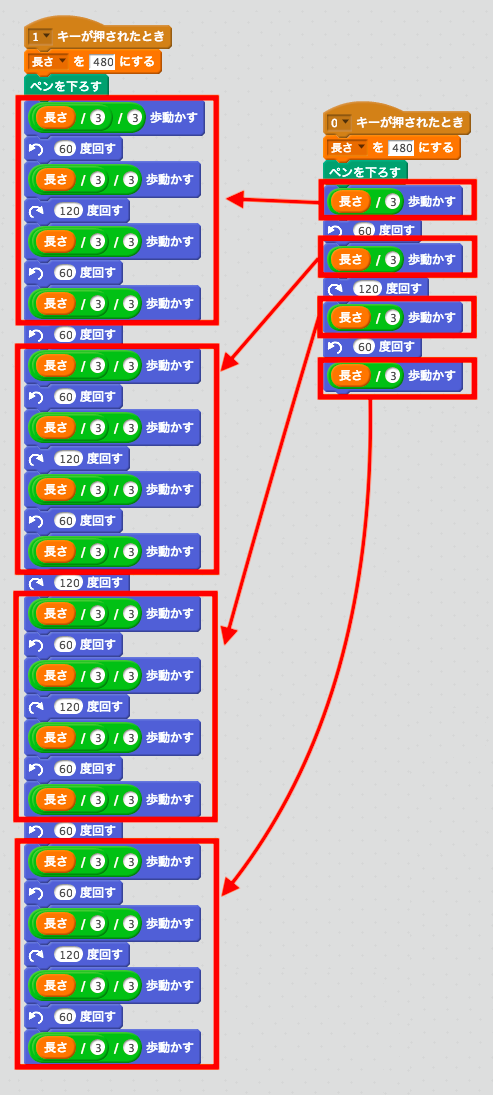
どうでしょうか?このように比較すると、同じ処理が繰り返し出てくるのが分かると思います。1キーを押して再帰回数1回のプログラムを実行してみましょう。

再帰回数1回のコッホ曲線が描けました。
2-2. 再帰プログラムで描いてみる
先ほどの再帰回数が1のプログラムと、再帰回数0回のプログラムの比較から以下のようなことが分かりました。
・再帰回数1のプログラムには、再帰回数0のプログラムが含まれている
・再帰回数1の直線の長さは、再帰回数0のプログラムの直線の長さの3分の1
と考えると、コッホ曲線は次のように定義できます。
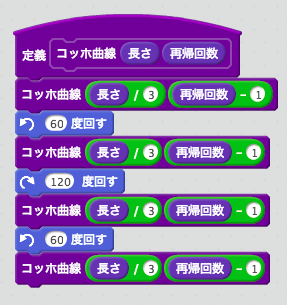
ですが、このままだと「●歩動く」がありませんね。どこかに入れる必要があります。
そこでコッホ曲線の一番最初の状態、つまり再帰回数0回の一つ前の状態=これを仮に再帰回数-1回の時を考えてみましょう。この時は直線になります。そこで、「再帰回数が0より小さい時」の定義も追加しましょう。再帰回数が-1回の時はただの直線になるようにします。
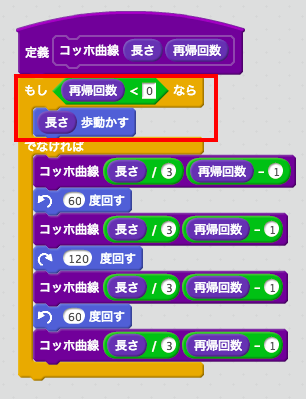
はい。これでコッホ曲線の定義は完成です。コッホ曲線を描くためにはペンの上げ下げが必要なので、ペンの動きも定義に追加しておきます。

では次にコッホ曲線を描くプログラムを作りましょう。数字キーで再帰回数が設定できるようにしたいと思います。下の図のように、0から9までの再帰回数でコッホ曲線が描けるようにしました。

再帰回数が増えてくると、プログラムが遅くなってくるのでターボモードで実行しましょう。
4キーを押すと再帰回数4回のコッホ曲線が描けました!
完成したプログラムはこちらです。1、2、3、4、5・・・とキーを押していくとどんどん形が変化して面白いですよ。
3. まとめ
今回は、再帰プログラムを作ってフラクタル図形「コッホ曲線」を作りました。
再帰プログラムはいきなり定義を見るとよく分からなくなってしまいます。学習のためには、まずは再帰を使わずに「無理やり」プログラムを書いてみるというのもいいと思います。
無理やり書いたものの中から規則性をみつけ、それを再帰プログラムにしてみるといいと思います。















